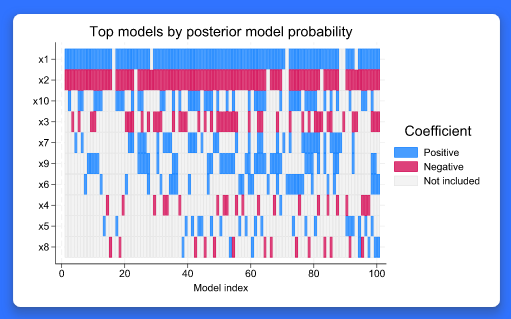
전통적으로, 사용자는 모형을 선택하거나 분석의 적합도를 평가합니다. 이 결과들은 사용자가 선택한 모형에 의존합니다. 다수의 그럴듯한 모형이 주어졌을 때, 전통적인 접근은 신뢰성이 떨어질 수 있습니다. 모형평균화기법은 다수의 모형을 기반으로 분석의 적합도를 평가하고 모형의 불확실성을 설명할 수 있습니다. BMA는 베이지안 법칙에 따라 생성한 다양한 자료를 적용하여 모형의 불확실성을 설명합니다. 그리고 이러한 불확실성은 회귀모형에서 반드시 포함되어야 할 독립변수(예측변수)에 대한 불확실성의 정도를 설명합니다. 새로운 bmaregress은 선형회귀모형의 BMA를 수행합니다. 그리고 이를 통해 통계적 추론, 예측 그리고 사용자의 목적에 따라 심지어는 모형선택에 활용될 수 있습니다. 예를 들면, Y변수를 종속변수로 하고 x1, x2를 독립변수로 하는 BMA 회귀모형을 아래와 같이 추정한다고 가정해봅시다. . bmaregress y x1 x2 독립변수를 모형 내 포함하거나 제외하는 경우의 수를 고려하면, x1, x2가 포함된 모형은 총 4개의 가능한 조합에 따른 모형을 생각할 수 있습니다. 그리고 가능한 모형들의 조합으로 관측된 자료를 얼마나 잘 설명하는지 알 수 있습니다. 사용자는 이 결과를 통해 다양한 사전분포를 선택하여 모형 혹은 독립변수(예측변수)의 중요도에 대한 효과를 탐색할 수 있습니다. 사후추정명령어는 모형 확률 추정, 독립변수 중요도 평가, 모형 복잡성 탐색, 예측 평균추정, 예측력 평가, 회귀계수 통계적 추론을 수행합니다. 기능의 흥미로운 점은 무엇일까요? 어떠한 상용 소프트웨어도 BMA 패키지를 제공하고 있지 않습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 대부분의 모든 사용자는 선형회귀모형을 사용합니다. bmaregress는 선형회귀모형을 위한 BMA로 독립변수(예측변수)가 활용되는 모든 영역의 연구자들에게 모형의 불확실성을 설명할 수 있습니다.

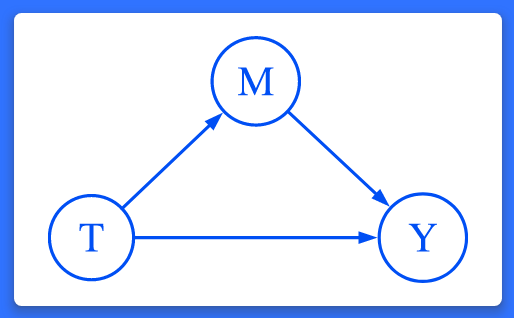
인과적 추론은 결과변수에 대한 처치효과를 정의하고 평가하는 목적이 있습니다. 인과매개분석은 이러한 처치효과가 어떻게 발생하는지 더 탐색하는데 목적이 있습니다. 매개효과의 예를 들면 운동은 호르몬의 수준을 증가시키고 이는 차례로 삶의 질(well-being)을 증진시킵니다. 수입 제한량(quota)은 국내 기업의 시장지배력을 증가시키고 차례로 상품의 가격을 증가시킵니다. 연구자들은 자주 이러한 관계를 아래와 같이 인과그림으로 시각화 합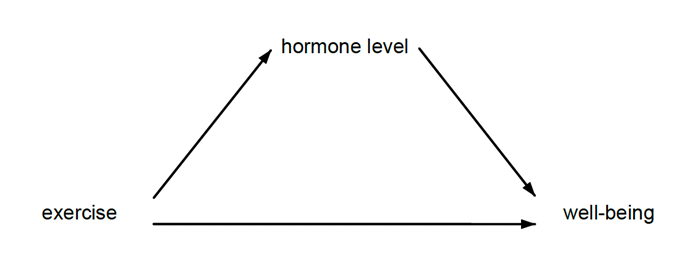니다. 새로운 mediate 명령어는 처치가 종속변수에 미치는 총효과를 추정하고 직접효과와 매개효과라고 부르는 간접효과(예를 들면 호르몬)를 분해할 수 있습니다. 사실, 직접 및 간접효과 뿐만 아니라 연구자가 관심을 가지고 있는 가설에 따라 다양한 유형의 효과분해를 수행할 수 있습니다. 또한, estate proportion 명령어는 매개변수를 통해 발생하는 총효과의 비율을 보고합니다. mediate 명령어는 다양한 변수유형에 적용할 수 있습니다. 결과변수, 매개변수가 연속형, 이분형, 카운트형 일 수도 있고 처치변수는 연속형, 이분형, 다범주(multivalued)일 수 있는데 이러한 유형을 모두 지원합니다. 기능의 흥미로운 점은 무엇일까요? mediate 명령어는 위에 언급한 결과변수, 매개변수, 처치변수 유형의 24개 조합을 지원하여 실제 연구에서 발생하는 많은 상황에서 활용할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 인과추론과 관련된 질문은 사실상 모든 분야에서 자연스럽고 중요한 질문입니다.

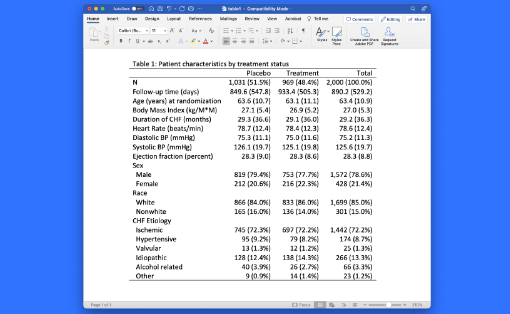
새로운 dtable 명령어는 기술통계량 표를 생성합니다. dtable은 연속형 또는 범주형 변수의 요약통계량을 보고합니다. 사용자는 각 변수들에 대해 어떠한 통계량를 보고할지 선택할 수 있습니다. 예를 들어, 평균, 표준편차, 중앙값, 사분범위, 백분율 및 비율과 더 다양한 통계량을 선택합니다. 사용자는 또한 범주(혹은 그룹)에 따른 변수의 통계량을 쉽게 비교할 수 있습니다. dtable로 생성된 표는 다양한 요소를 사용자가 수정할 수 있습니다. 예를 들면, 보고할 통계량, 숫자 그리고 문자형식, 노트, 제목, 라벨 그리고 더 많은 요소를 선택하고 수정할 수 있습니다. 표는 Microsoft Word, Microsoft Excel, HTML, Markdown, PDF, LaTeX, SMCL, plain text 파일로 직접 내보낼 수 있습니다. 기능의 흥미로운 점은 무엇일까요? dtable 명령어는 대부분의 모든 연구문서에 포함되는 첫번째 표인 “Table 1”을 쉽게 생성해 줍니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 이러한 표는 탐색적 분석을 하거나 출판을 위한 표를 생성하는 모두에게 유용합니다.

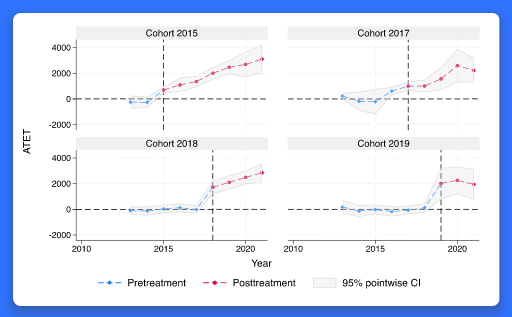
DID 모형은 반복측정 자료에서 처치그룹의 평균처치효과(ATET)를 추정하는데 사용됩니다. 처치효과는 혈압에 영향을 미치는 약의 효과나 취업자의 교육프로그램 효과 등이 그 예가 될 수 있습니다. 기존 teffect 명령어에서 지원하는 일반적인 횡단면 분석과 달리, DID 분석은 ATET 추정 시 반복측정된 통제집단과 시간의 효과를 분석합니다. 이질적 처치효과 DID 모형은 추가적으로 그룹내 기간에 따른 효과나 서로 다른 시점에서 처치된 그룹의 처치효과와 같은 처치효과의 이질성을 설명합니다. 몇몇 학군(school districts)에서 학생의 건강상태를 향상시키기 위한 운동과 식습관 프로그램이 도입되었다고 가정해봅시다. 그리고 프로그램이 학군에 따라 도입된 시점이 다르다고 합시다. 이 경우 학생의 건강상태에 영향을 미치는 프로그램의 효과가 도입된 시점 및 정착한 시점과 관계없이 같다고 가정하는 것이 적절할까요? 아마 그렇지 않을 것입니다. 이질적 처치효과 DID 모형은 이러한 효과의 잠재적 차이를 설명하는데 활용될 수 있습니다. 새롭게 추가된 hdidregress, xthdidregress 명령어는 이질적 처치효과 DID 모형을 추정합니다. hdidregress 명령어는 반복횡단면 자료(repeated-cross-sectional data), xthdidregress 명령어는 횡단면/패널 자료(longitudinal/panel data)에 적합합니다. 기능의 흥미로운 점은 무엇일까요? 이질적 처치효과 DID는 최근에 전세계에서 열린 Stata 컨퍼런스에서 매우 유명하고 관심있는 주제였습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 인과추론과 관련한 질문은 사실상 모든 분야에서 자연스럽고 중요한 질문입니다.

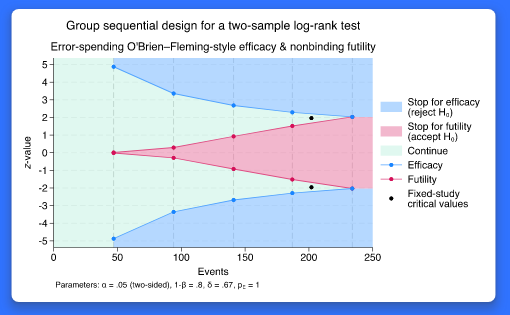
GSDs는 적응형 설계(adaptive design)의 유형으로 연구자들이 처치가 효과적이거나 효과적이지 않다는 강력한 증거를 발견했을 때 실험을 일찍 중단하는 것을 허용합니다. 연구자가 화학요법(chemotherapy)이 종양 치료에 효과가 있는지 검증하기 위한 연구를 설계하고 이를 위해 몇 년에 걸쳐 자료를 수집한다고 가정해 봅시다. 이 경우 모든 시점이 다 측정되기까지 기다린 이후 자료를 분석하기 보다는 자료가 수집될 때마다 중간 분석하는 것이 더 선호될 수 있습니다. GSDs는 이러한 접근을 가능하게 합니다. 각 중간분석은 계속 자료수집을 해야 할지 혹은 중단해도 되는지에 대한 정보를 제공합니다. 만약 화학요법 효능에 대한 매우 강력한 증거가 발견된다면, 자료수집은 일찍 중단될 수 있습니다. 자료수집은 또한 화학요법의 효능이 없다는 매우 강력한 증거가 발견되는 경우에도 일찍 중단될 수 있습니다. 이러한 결과는 추가적인 피실험자가 부적절한 처치에 노출되는 것을 방지할 수 있습니다. Stata 18에서는 GSDs를 위한 통합적인 명령어를 제공합니다. 새로운 gsbounds 명령어는 효능성(efficacy)과 무효능성(futility) 한계값을 분석(혹은 관찰)의 횟수, 요구되는 전체 1종 오류 및 검정력을 기반으로 계산합니다. 연구자는 gsbounds에서 제공하는 7개 한계-계산법을 선택할 수 있습니다. 한계-계산법은 연구자가 이전 분석에서 전통적 혹은 오류분배 방법을 원하는지 그리고 더 보수적인 기준을 적용할지 혹은 덜 보수적인 기준을 적용할지에 따라 선택할 수 있습니다. 새로운 gsdesign 명령어는 효능성(efficacy)과 무효능성(futility) 한계값을 계산하고 평균, 비율, 생존함수 검정을 위한 중간 및 최종분석에 필요한 표본크기를 제공합니다. GSDs 통합 명령어에서는 모든 중간 그리고 최종분석들 사이의 한계를 쉽게 시각화하기 위한 그래프를 제공합니다. 기능의 흥미로운 점은 무엇일까요? GSDs 수행은 매우 사용자 친화적입니다. 명령어 문법은 기존의 power 명령어와 유사한 직관적 문법구조를 따르고 있으며 명령어가 아닌 마우스 클릭으로도 쉽게 접근할 수 있습니다. 표본크기 계산은 gsdesign 명령어를 통해 기본적으로 제공하는 평균, 비율, 생존함수 검정을 넘어 사용자정의 방법을 통해 확장할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 약학분야 사용자에게 유용합니다. 또한 임상실험연구 설계를 하는 연구자들에게도 흥미로울 것입니다. 왜냐하면 GSDs는 임상심리학자와 다른 의료연구자들로 확장될 수 있기 때문입니다.

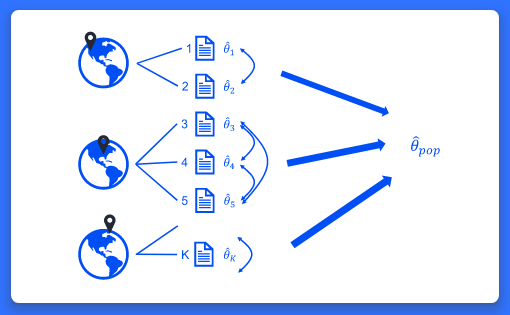
연구가들이 다수 연구들의 결과들을 분석하고자 할 때, 결과를 통합하고 전체효과크기를 추정하기 위해 메타분석을 사용합니다. 기존의 meta 통합명령어는 이러한 일반적인 메타분석과 다변량 메타분석을 제공합니다. 때때로 보고된 효과크기는 지리적 위치(주 혹은 국가)나 행정적 단위(학군)와 같은 상위수준그룹 안에 내포(nested)되어있습니다. 동일그룹(예를 들어 학군) 내 효과크기는 유사할 가능성이 있으며 그렇기 때문에 그룹에 종속적입니다. 이러한 경우, 연구자는 다층메타분석을 사용할 수 있습니다. 다층 메타분석의 목적은 전체효과 크기를 통합하는 것뿐만 아니라 그룹에 따른 종속성을 설명하고 서로 다른 위계적 수준들 사이의 효과크기의 변동성을 측정하는데 있습니다. 새로운 meta meregress와 meta multilevel 명령어는 다층 메타분석을 수행합니다. 연구자가 두가지 학습지도 방법이 수학 성적에 미치는 효과 y, y변수의 표집오차인 se변수를 기존연구를 통해 수집했다고 가정해봅시다. 효과크기는 학교에 내포되어 있고 학교는 또한 학군에 내포되어 있습니다. 이러한 경우 연구자는 3수준 확률절편 모형을 아래와 같이 추정할 수 있습니다. . meta meregress y || district: || school:, essevariable(se) or . meta multilevel y, relevels(district school) essevariable(se) 만약, 연구자가 수집한 자료에 공변량이 있고 공변량의 확률계수를 도입하고자 한다면 아래와 같이 추정할 수 있습니다. . meta meregress y x1 x2 || district: x1 x2 || school:, essevariable(se) 모형 추정 후, 사후추정 명령어를 통해 다층 이질성 통계량, 추정된 확률효과 공분산 행렬 등을 추가적으로 추정할 수 있습니다. 기능의 흥미로운 점은 무엇일까요? 명령어가 매우 단순합니다. 또한 meta meregress는 확률효과 제약을 매우 유연하게 적용할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 모든 분야의 연구자들은 기존의 연구 결과들을 통해 전체 효과크기를 추정하고 싶어 할 것입니다.

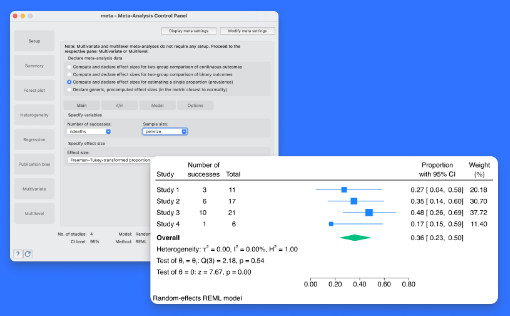
meta esize 명령어는 이표본 이분형 혹은 연속형 자료에 대한 메타분석을 수행합니다. 이제, 비율 메타분석 혹은 유병률 메타분석으로 알려진 일표본 이분형 자료의 메타분석을 수행할 수 있습니다. 이러한 자료 유형은 메타분석 연구에서 공통적으로 하나의 비율로 추정되는 각 연구들의 결과를 통합할 때 발견됩니다. 예를 들어, 연구자가 특정한 질병에 대한 유병률이나 고등학교 자퇴학생의 비율과 같은 연구들에 관심이 있을 수 있습니다. 이러한 경우, 메타분석에서 전형적으로 활용되는 Freeman–Tukey 변환비율이나 logit 변환비율과 같은 효과크기를 사용할 수 있습니다. meta esize 명령어 사용 후, 추가분석을 위해 기존 meta 통합명령어를 사용할 수 있습니다. 예를 들어, meta forestplot 명령어를 활용하여 숲그림(forest plot)을 생성하고 forestplot의 subgroup( ) 옵션을 추가하여 하위집단 분석을 수행할 수 있습니다. 또한 meta summarize 명령어를 통해 메타분석자료를 요약하거나 meta funnelplot 명령어로 깔대기그림(funnel plot)을 생성할 수도 있습니다. 기능의 흥미로운 점은 무엇일까요? 유병률 연구를 위한 메타분석은 기존 메타분석에 추가되기를 요청한 대부분의 사용자에게 유용할 것입니다. 많은 사용자들은 이런 종류의 연구들을 분석하기를 기대하고 있었습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 모든 분야의 연구자들은 기존의 연구 결과들을 통해 전체효과크기를 추정하고 싶어 할 것입니다.

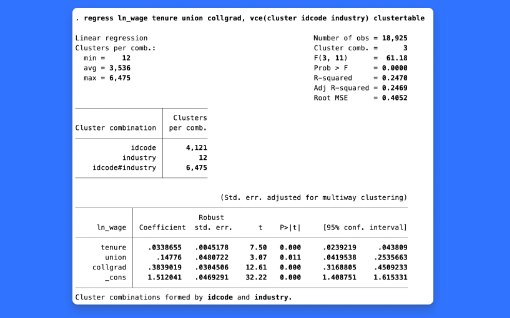
연구에서 신뢰성있는 표준오차는 적절한 추론을 하기위해 매우 중요한 부분입니다. Stata 18은 regress, areg, xtreg, fe 와 같은 선형모형 들에서 새로운 표준오차와 신뢰구간을 제공합니다. 새로운 방법은 대표본 근사방법이 적절하지 않을 때 더 좋은 추론을 제공합니다. 아마 연구자는 몇개 안되는 그룹을 가지거나 그룹내 관측치가 불균형한 군집자료를 가지고 있을 수 있습니다. 이 경우, 연구자는 vce(hc2 clustvar) 옵션을 추가하여 HC2 군집 로버스트 표준오차를 추정할 수 있습니다. 혹은 연구자가 한 개 이상의 그룹식별변수를 가지고 있다면 이제 vce(cluster clustvar1 clustvar2 …)을 적용하여 다원(multiway) 군집표준오차를 추정할 수 있습니다. 기능의 흥미로운 점은 무엇일까요? 다양한 상황에서 가장 적절한 표준오차의 선택과 관련한 주제는 소셜미디어에서 매우 활발하게 논의되고 있습니다. Stata 18가 이제 연구자들에게 선택할 수 있는 더 많은 옵션을 제공할 수 있어서 매우 기쁩니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 대부분의 모든 연구자들은 선형모형을 활용하고 있으며 그들에게 새로운 표준오차 추정방법은 매우 흥미로울 것입니다.

와일드 군집 부트스트스랩은 연구자의 군집자료가 몇 개 안되는 그룹을 가지고 있거나 그룹내 관측치가 불균형하거나 두가지를 모두 가지고 있을 때 강건한(robust) 추론을 위한 또 하나의 새로운 옵션을 제공합니다. 새로운 wildbootstrap 명령어는 선형회귀모형의 모수에 대한 단순 및 선형조합가설을 검정하기 위한 와일드 클러스터 부트스트랩 p값과 신뢰구간을 추정합니다. 사용자는 선형회귀모형, 큰 더미변수를 가진 선형회귀모형, 패널데이터 고정효과 모형에서 와일드 군집 부트스트랩 통계량을 아래와 같이 간단하게 수행할 수 있습니다. . wildbootstrap regress y x1 x2 … or . wildbootstrap areg y x1 x2 …, absorb(x3) or . xtset id . wildbootstrap xtreg y x1 x2 … 기능의 흥미로운 점은 무엇일까요? 와일드 군집 부트스트랩 통계량은 선형모형에서 로버스트 추론을 위한 많은 새로운 도구를 사용자에게 제공한다는 점에서 앞서 언급한 새로운 표준오차에 대한 관심에 잘 맞는 기능에 해당합니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 대부분의 모든 연구자들은 선형모형을 활용하고 있으며 로버스트추론을 위한 와일드 군집 부트스트랩은 그들에게 매우 흥미로울 것입니다.

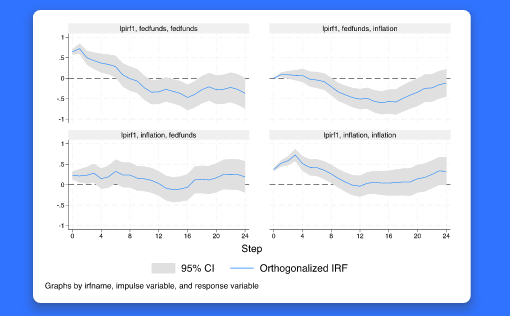
새로운 lpirf 명령어는 IRFs의 국지적 투영을 지원합니다. 국지적 투영은 시계열 분석에서 결과변수에 영향을 미치는 충격의 효과를 추정합니다. 예를 들어, 연구자가 이자율의 예상치 않은 변화가 국가생산과 인플레이션율에 미치는 효과를 평가하고자 할 수 있습니다. 이때, 아래와 같이 명령을 입력하면, y1과 y2의 IRFs의 국지적 투영 추정치를 얻을 수 있습니다. . lpirf y1 y2 사용자는 또한 exog( ) 옵션을 추가하여 외생변수의 효과인 동적 승수함수를 추정을 할 수 있습니다. 새로운 lpirf 마치 그래프, IRFs 표, 직교화 IRFs, 동적 승수함수를 생성하는 기존의 irf 명령어처럼 작동합니다. 앞서 언급한 선형모형의 로버스트 표준오차는 IRF 추정에서도 중요합니다. 따라서, 로버스트와 Newey–West 표준오차를 함께 지원합니다. 기능의 흥미로운 점은 무엇일까요? IRFs 국지적 투영은 VAR 모형을 기초로 하는 IRFs의 대안을 제공합니다. 국지적 투영은 모형에 의해 제약되지 않습니다. 그렇기 때문에 더 유연한 IRF 계수를 제공합니다. 국지적 투영은 또한 가설검정을 쉽게 할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 시계열 분석을 하는 경제학, 정치학, 금융분야 그리고 공공정책 분야에서 유용하게 활용될 수 있습니다.

연구자들은 상품에 대한 수요를 추정하는데 관심을 가지고 있습니다. 새로운 demandsys 명령어는 상품의 수요를 계산하고 가격 및 지출 탄력성에 의해 수요가 얼마나 민감하게 반응하는지 측정하는 방대한 도구를 제공합니다. 사용자는 demandsys 명령어를 통해 8개의 수요시스템 모형을 추정할 수 있습니다. - Cobb–Douglas 모형 - 선형지출시스템 모형 - 기본 트랜스로그 모형 - 일반화 트랜스로그 모형 - 완전[1] 수요모형 - 일반화 완전수요 모형 - 이차 완전수요모형 - 일반화 이차 완전수요모형 함께 제공하는 estat elasticities 명령어는 다양한 탄력성을 추정할 수 있습니다. 추정가능한 탄력성은 지출탄력성, 비보상 가격 및 교차가격 탄력성, 비보상 가격 및 교차가격 탄력성으로 이를 통해 가격 및 지출에 따라 어떻게 수요가 민감하게 변화하는지 탐색할 수 있습니다. 기능의 흥미로운 점은 무엇일까요? demandsys 명령어에서 제공하는 8개의 수요시스템은 연구자들에게 그들의 경험적 가정에 따라 수요시스템을 선택할 수 있는 다양성을 제공합니다. 어떤 분야 및 사용자에게 유용할까요? 경제, 기업, 마케팅, 경영분야의 연구자들에게 수요시스템은 매우 유용할 것입니다.

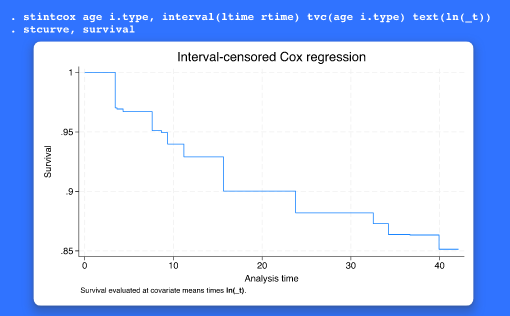
사건사 자료(혹은 생존자료)에서 구간중도절단은 암 재발과 같은 관심있는 사건이 언제 일어났는지 특정한 시간은 관찰할 수 없으나 언제부터 언제까지 사이에 일어났는지 알고 있을 때 발생합니다. 기존의 stintcox 명령어는 준모수적 구간중도절단 Cox 비례위험 모형을 추정합니다. Stata 18에서는 stintcox 명령어를 통해 시변 공변량을 추가적으로 모델링할 수 있습니다. 그리고 stintcox는 이제 개체의 각 검사에 따른 다중레코드 구간중도절단 자료에서도 추정을 지원합니다. 이러한 자료구조는 각 검사시간에 따라 공변량의 값이 기록된 자료로 시변 공변량를 쉽게 저장할 수 있습니다. stintcox 명령어는 새로운 옵션인 tvc(varlist_t), texp(exp)를 제공합니다. tvc(varlist_t) , texp(exp)는 시간상호작용 공변량을 쉽게 모형에 포함하는 옵션으로 공변량과 tvc( )는 설정된 공변량과 texp( )는 설정된 시간함수의 사이의 상호작용을 모델링 합니다. 모형을 추정한 후에, 시변 공변량을 적절히 설명하기 위한 표준적이고 특수한 사후명령어도 지원합니다. 사용자는 새로운 estat gofplot 명령어를 통해 적합도 그래프를 생성할 수 있습니다. 또한 상대위험을 예측할 수 있습니다. 그리고 stcurve을 이용하여 생존함수나 그와 연관된 그래프를 쉽게 생성할 수 있습니다. 다중레코드 자료를 가지고 있을 때, 사용자는 새로운 atmeans 옵션을 통해 설정한 시간에 따른 공변량의 평균을 평가하거나 새로운 atframe(framename) 옵션을 통해 framename 프레임에 있는 변수의 값에 따라 함수를 평가할 수 있습니다. 기능의 흥미로운 점은 무엇일까요? 구간중도절단 생존자료에 적합한 비모수 모델링은 최근 몇년동안 있었던 방법론적 진보를 통해 구현된 stintcox 명령어 외에는 불가능했었습니다. 그리고 방법론적 발전과 함께 이제 시변 공변량 추정이 명령어에 통합되었습니다. 어떤 분야 및 사용자에게 유용할까요? 생존 및 기간분석을 하는 생물통계학, 경제학, 역학, 의학, 정치학, 보건학 연구자 및 연구기관에서 유용하게 활용될 수 있습니다.

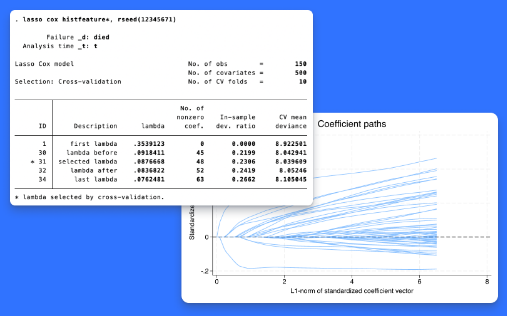
Stata는 매우 많은 잠재적 공변량이 있을 때 예측 및 모형선택을 위한 lasso를 제공하였습니다(여기서 "많다"의 의미는 100개, 1000개 혹은 그 이상을 의미합니다). 기존 lasso 명령어는 선형, 로짓, 프로빗 그리고 포아송 모형을 지원했습니다. Stata 18에서는 새롭게 Cox 비례위험모형을 lasso 에서 지원합니다. lasso cox 명령어는 생존자료에서 lasso 기법을 이용하여 변수를 선택하고 Cox 모형을 추정할 수 있습니다. 또한 elasticnet cox는 신축망(elastic net)을 아용하여 공변량 선택 및 Cox 모형을 추정할 수 있습니다. lasso cox 와 elasticnet cox 명령어를 수행한 후, 사용자는 predict 명령어를 이용하여 위험비를 예측할 수 있습니다. 또한 생존, 위험 혹은 누적 위험함수 그래프를 생성하는 stcurve 등의 생존분석 사후명령어를 lasso cox 와 elasticnet cox 결과를 설명하는데 활용할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 생존 및 기간분석을 하는 생물통계학, 경제학, 역학, 의학, 정치학, 보건학 연구자 및 연구기관에서 유용하게 활용될 수 있습니다.

역학연구자들은 개체가 관심을 가지는 결과를 발생시키는 두가지 높은 위험에 노출되었을 때 두 노출의 상호작용이 어떻게 영향을 미치는지 관심을 가집니다. 예를 들어, 흡연과 석면에 노출되었을 경우 어떻게 두 요인이 상호작용하여 폐암위험을 증가시키는지에 대해 조사하고 싶을 수 있습니다. 새롭게 추가된 reri 명령어를 이용하면, 연구자는 다른 위험요인을 설명과 동시에 상대위험의 가산적 모형을 통해 이원상호작용을 측정할 수 있습니다. 연구자들은 또한 로지스틱, 이항 일반화선형, 포아송, 음이항, Cox, 모수생존, 구간중도절단 모수생존, 구간중도절단 Cox 모형과 같은 다양한 지원모형을 선택할 수 있습니다. 그리고 3가지 관련 통계량(RERI, 기여분율, 시너지 지표)을 통해 흡연과 석면노출 사이의 상호작용을 가산적 모형을 통해 평가할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 역학, 의학, 보건학 연구자 및 연구기관에서 유용하게 활용될 수 있습니다.

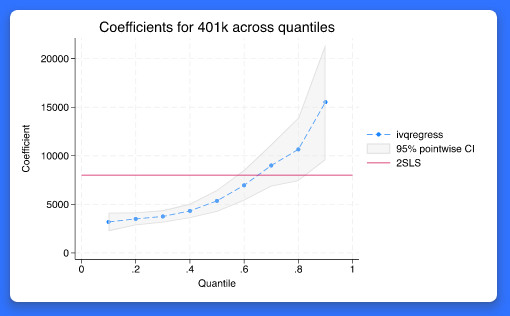
연구자들은 단순히 공변량의 효과에 따른 종속변수의 평균이 아니라 분위수에 관심을 가질 때가 있습니다. 이 경우 분위회귀가 사용됩니다. 예를 들어, 연구자가 학생의 성적등급 분포를 모델링하고 공변량이 변화할 때 등급이 어떻게 변화하는지에 관심이 있습니다. 이경우 기존의 qreg 명령어로 분위회귀모형을 추정하게 됩니다. 그러나 관심을 가지는 공변량이 내생적이면 어떻게 될까요? 이러한 내생성은 연구참여자의 자기선택, 중요변수 누락이나 측정오차에 의해 발생할 수 있습니다. 새로운 ivqregress 명령어는 종속변수의 분위수를 추정하고 동시에 도구변수를 사용하여 내생성 문제를 고려할 수 있습니다. 도구변수 분위회귀모형을 추정한 이후에 사용자는 estat coefplot 명령어를 통해 분위수 간 계수를 시각화 할 수 있습니다. 그리고 내생성 검정을 위한 estat endogeffects 명령어, 약한 도구변수를 위한 이중 로버스트 신뢰구간을 estat dualci 명령어로 추정할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 분위회귀는 모든 분야에서 잘 알려진 방법입니다. 특히 경제, 공공행정, 정치학, 공공보건, 경영 분야 연구자들에게 매우 흥미로울 것 입니다.

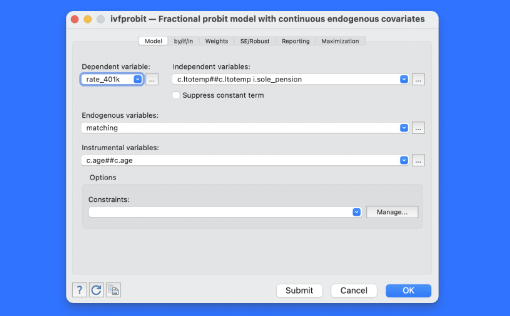
비율종속변수는 많은 자료에서 공통적으로 발견할 수 있습니다. 예를 들어, 401(k) 연금 참여자 비율, 표준검사 통과율, 지출비율 등과 같은 비율변수가 그 예에 해당합니다. 비율반응변수 모형은 이러한 0~1사이에 있는 종속변수를 모델링하는 유연하고 직관적인 방법입니다. 비율종속변수를 다루는 선형모형은 예측치가 0과 1값 밖에 있는 값이 산출되는 문제가 있으며, 로그오즈모형은 0과 1값을 정의할 수 없는 문제가 있습니다. 이러한 비율반응변수 모형은 기존의 fracreg 명령어를 이용하여 추정할 수 있습니다. 관심을 가지는 공변량이 내생적이면 어떻게 될까요? 새로운 ivfprobit 에서는 사용자가 비율종속변수를 모델링하고 하나 혹은 그 이상의 내생공변량을 동시에 처리할 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 비율자료는 모든 연구분야에서 공통적으로 발견할 수 있습니다.

Stata 16 부터, Stata는 메모리에서 다수의 데이터를 관리하는 기능을 지원해왔습니다. 다수의 데이터를 다루는 경우, 각 자료는 프레임안에 담겨집니다. 자료가 서로 관계가 있으면, 사용자는 frlink 명령어를 이용하여 현재 프레임과 관계가 있는 프레임 내 변수 및 관측치를 서로 연결할 수 있습니다. Stata 18에서는, 새로운 fralias add 명령어를 통해 사용자가 연결된 프레임간 별칭(alias) 변수를 생성하여 각각의 프레임에 저장된 변수를 분석에 쉽게 사용할 수 있습니다. 별칭 변수는 다른 프레임에 있는 변수를 현재프레임에 저장하는 것처럼 보이지만, 실제로는 원래 프레임에 저장되어 있으며, 별칭변수는 아주 작은 메모리를 차지합니다. 별칭변수 사용이 얼마나 쉬운지 보기 위해 다음과 같은 자료가 있다고 가정해봅시다. y는 현재 프레임 있는 변수이고 x변수는 frame2라는 이름의 프레임에 있는 변수로 현재 프레임과 연결되어 있습니다. x변수의 별칭을 현재 프레임에서 생성하기 위해 아래와 같이 수행합니다. . fralias add x, from(frame2) 그러면 사용자는 x가 현재 프레임에 있는 것처럼 아래와 같이 수행할 수 있습니다. . regress y x 어떤 분야 및 사용자에게 유용할까요? 모든 분야의 사용자들에게 유용합니다. 특히 메모리에서 다수의 자료를 작업하는 사용자는 이 새로운 기능이 매우 흥미로울 것 입니다.

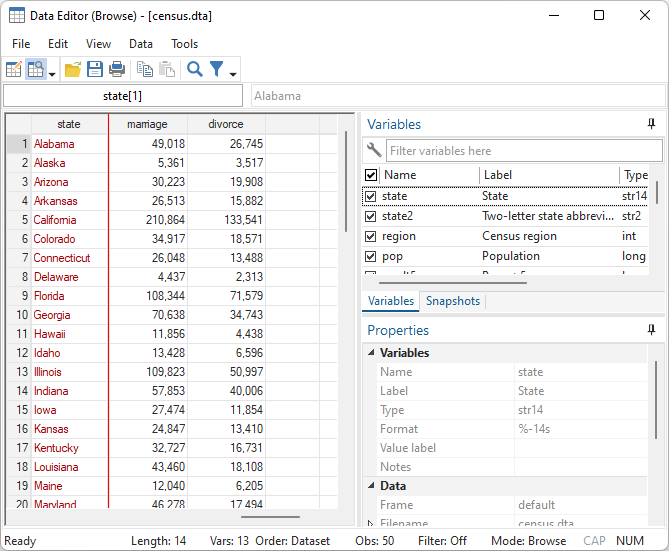
데이터 편집기는 Stata 18에서 많은 기능들이 향상되었습니다. 향상되거나 추가된 기능은 다음과 같습니다. 행, 열 고정핀 기능. 행 혹은 열의 고정핀은 자료를 스크롤하더라도 핀으로 고정된 행과 열은 스크롤되지 않습니다. 이 기능은 시각적으로 비교하고자 하는 자료가 서로 스크롤을 해야할때 매우 유용합니다. 대표적으로 ID 변수는 이러한 고정핀을 사용하는 것이 매우 유용할 수 있습니다. 문자값을 위한 셀 크기 재변경. 사용자가 셀 크기보다 큰 문자값을 수정할 때, 편집기에서 스크롤 할 필요없이 문자가 잘 보일 수 있도록 크기를 재변경합니다. 잘린 문자열을 위한 툴팁기능. 어떠한 셀 값이 셀 너비보다 너무 크면 값이 잘려서 보입니다. 이러한 경우 마우스를 잘린 텍스트 셀 위에 올려놓으면 전체값을 보여주는 툴팁을 보여줍니다. 비율너비 글자체 지원. 데이터 편집기가 이제 비율너비 글자체 지원합니다. 이 기능은 자료의 가독성을 향상시키고 스크롤 필요없이 한 화면에 많은 변수를 보여 줄 수 있습니다. 열 상단에 변수라벨 보여주기. 변수라벨이 이제 선택된 변수이름 밑 열상단에 표시됩니다. 데이터 편집기에서 변수의 이름이 짧고 성격을 파악하기 어려운 경우 사용자는 따로 변수라벨을 확인합니다. 이제는 편집기 열상단에서 한 번에 확인할 수 있어 매우 유용합니다. 값라벨 보기/숨기기 단축키. 숫자변수의 값라벨 보기/숨기기를 단축키를 통해 빠르게 켜고 끌 수 있습니다. 어떤 분야 및 사용자에게 유용할까요? 모든 사용자에게 유용합니다.

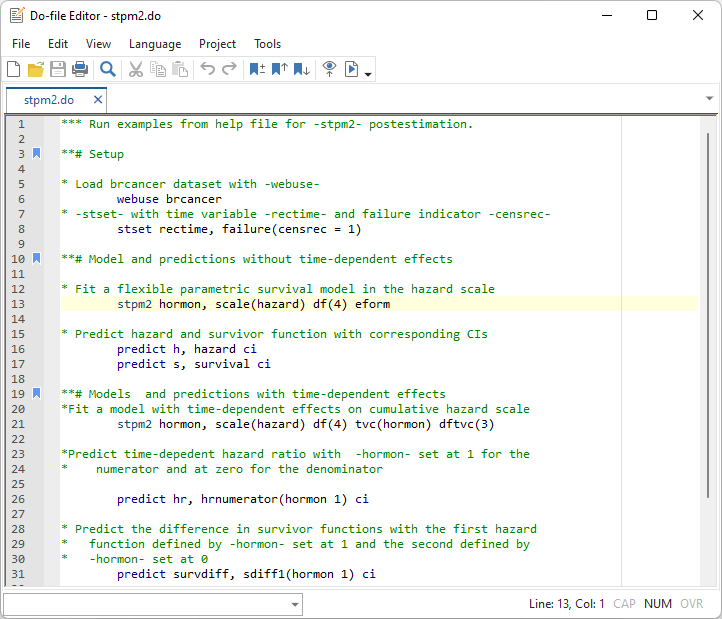
Stata 18에서 Do 파일 편집기 또한 향상되었습니다. 향상되거나 추가된 기능은 다음과 같습니다. 자동저장기능. Do 파일 편집기에서 작업하고 있는 문서는 주기적으로 백업파일에 저장됩니다. 자동저장은 아직 저장하지 않은 새로운 문서 또한 포함합니다. 만약 사용자가 작업한 문서를 저장하기 전에 컴퓨터의 전원이 꺼지거나 충돌이 발생하더라도, 이제는 저장하지 않은 결과를 복원할 수 있습니다. 사용자가 저장하지 않은 작업문서를 복원하고 싶다면, 단순히 Do 파일 편집기를 다시 열면 됩니다. 사용자가 작업하고 있는 폴더와 백업폴더가 동일하더라도 백업파일에서 복구를 요청하거나 가장 최근에 저장된 문서를 열 수도 있습니다. 백업파일 Do-파일 편집기를 통해 간단하게 확인 할 수 있으며, 사용자가 작업파일을 백업파일로 저장하지 않는다면 덮어쓰기 되지 않습니다. 사용자 정의 키워드 구문강조(Syntax-highlight). Stata의 Do 파일 편집기는 이제 사용자가 정의한 키워드에 대해 구문강조를 지원합니다. 이는 사용자가 선호하는 외부명령어(community-contributed commands)에 대해 구문강조를 허용합니다. 사용자가 구문을 강조하고자 하는 키워드 이름과 목록이 담긴 파일을 간단하게 생성하면, Stata는 이를 인식해 설정된 구문강조 환경설정(글자체, 색, 굵게 혹은 기울임 등)에 따라 구문을 강조하게 됩니다. 사용자는 또한 전역 키워드 정의파일을 생성하여 동일한 컴퓨터를 사용하는 모든 사용자에게 공유할 수 있습니다. 또한 각 사용자는 사용자만의 키워드 정의파일을 생 성하고 적용할 수 있습니다. 사용자 키워드 정의파일은 전역 키워드 정의파일과 함께 Do-파일 편집기에서 구문강조가 적용됩니다. 어떤 분야 및 사용자에게 유용할까요? 모든 사용자에게 유용합니다.

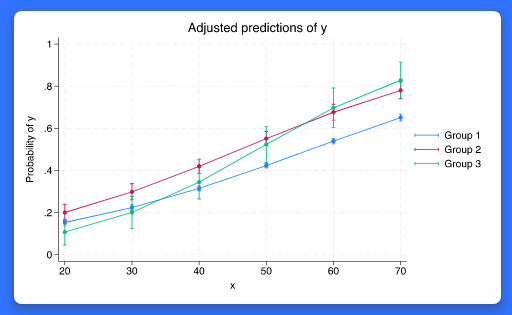
Stata 18에서는 새로운 그래프 스타일을 제공합니다. 새로운 그래프 색 및 요소구성(scheme; 혹은 Stata 그래프 테마)은 매우 많은 요청이 있었던 기능으로 아래 내용을 포함하고 있습니다. - 흰색 바탕 - 밝은 색 팔레트 업데이트 - 수평 y축 라벨 - 넓은 가로세로 비 - 특정그래프에서 동적 범례 배치 - 기타 등등 예를 들면, 기존의 막대 그래프 색 및 범례구성은 아래와 같습니다.

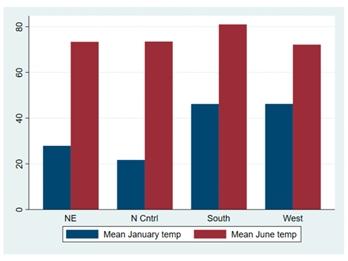
이번에 새롭게 제공하는 색 및 범례구성을 적용한 그래프는 아래와 같습니다.

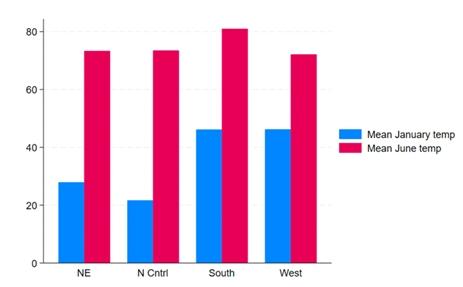
사실, Stata 18에서는 4가지의 새로운 그래프 색 및 요소구성을 제공합니다. : stcolor, stcolor_alt, stgcolor, stgcolor_alt 새로운 기본설정은 stcolor입니다. 그리고 다른 색 및 요소구성은 stcolor를 기초로 너비와 범례위치 등 값에 변화를 준 구성입니다. 어떤 분야 및 사용자에게 유용할까요? 모든 사용자에게 유용합니다.